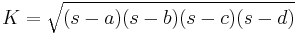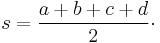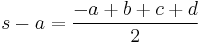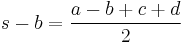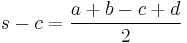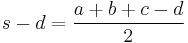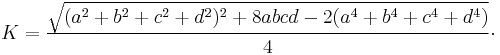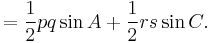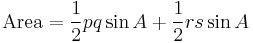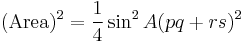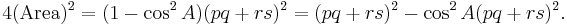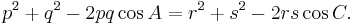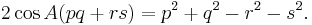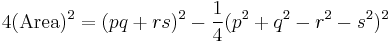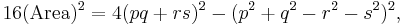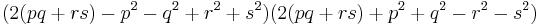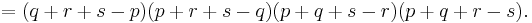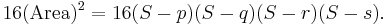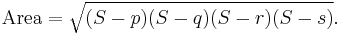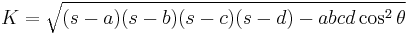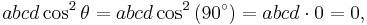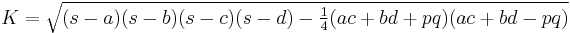Brahmagupta's formula

In Euclidean geometry, Brahmagupta's formula finds the area of any quadrilateral given the lengths of the sides and some of the angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle.

1 Basic form
2 Proof of Brahmagupta's formula
3 Extension to non-cyclic quadrilaterals
4 Related theorems
5 External links
6 References

Basic form

In its basic and easiest-to-remember form, Brahmagupta's formula gives the area K of a cyclic quadrilateral whose sides have lengths a, b, c, d as

$K=\sqrt{(s-a)(s-b)(s-c)(s-d)}$

where s, the semiperimeter, is

$s=\frac{a%2Bb%2Bc%2Bd}{2}\cdot$

$s-a= \frac{-a%2Bb%2Bc%2Bd}{2}$

$s-b= \frac{a-b%2Bc%2Bd}{2}$

$s-c= \frac{a%2Bb-c%2Bd}{2}$

$s-d= \frac{a%2Bb%2Bc-d}{2}$

This formula generalizes Heron's formula for the area of a triangle. In fact, Heron's formula may be derived from Brahmagupta's formula by allowing d to approach a value of zero. A triangle may be regarded as a quadrilateral with one side of length zero. From this perspective, as d approaches zero, a cyclic quadrilateral converges into a cyclic triangle (all triangles are cyclic), and Brahmagupta's formula converges into Heron's formula.

The assertion that the area of the quadrilateral is given by Brahmagupta's formula is equivalent to the assertion that it is equal to

$K=\frac{\sqrt{(a^2%2Bb^2%2Bc^2%2Bd^2)^2%2B8abcd-2(a^4%2Bb^4%2Bc^4%2Bd^4)}}{4}\cdot$

Brahmagupta's formula may be seen as a formula in the half-lengths of the sides, but it also gives the area as a formula in the altitudes from the center to the sides, although if the quadrilateral does not contain the center, the altitude to the longest side must be taken as negative.

Proof of Brahmagupta's formula

Here we use the notations in the figure to the right. Area of the cyclic quadrilateral = Area of $\triangle ADB$ + Area of $\triangle BDC$

$= \frac{1}{2}pq\sin A %2B \frac{1}{2}rs\sin C.$

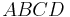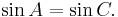But since $ABCD$ is a cyclic quadrilateral, $\angle DAB = 180^\circ - \angle DCB.$ Hence $\sin A = \sin C.$ Therefore

$\mbox{Area} = \frac{1}{2}pq\sin A %2B \frac{1}{2}rs\sin A$

$(\mbox{Area})^2 = \frac{1}{4}\sin^2 A (pq %2B rs)^2$

$4(\mbox{Area})^2 = (1 - \cos^2 A)(pq %2B rs)^2 = (pq %2B rs)^2 - \cos^2 A (pq %2B rs)^2.\,$

Solving for common side DB, in $\triangle$ ADB and $\triangle$ BDC, the law of cosines gives

$p^2 %2B q^2 - 2pq\cos A = r^2 %2B s^2 - 2rs\cos C. \,$

Substituting 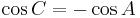$\cos C = -\cos A$ (since angles $A$ and $C$ are supplementary) and rearranging, we have

$2\cos A (pq %2B rs) = p^2 %2B q^2 - r^2 - s^2. \,$

Substituting this in the equation for the area,

$4(\mbox{Area})^2 = (pq %2B rs)^2 - \frac{1}{4}(p^2 %2B q^2 - r^2 - s^2)^2$

$16(\mbox{Area})^2 = 4(pq %2B rs)^2 - (p^2 %2B q^2 - r^2 - s^2)^2, \,$

which is of the form 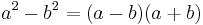$a^2-b^2 = (a-b)(a%2Bb)$ and hence can be written as

$(2(pq %2B rs) - p^2 - q^2 %2B r^2 %2Bs^2)(2(pq %2B rs) %2B p^2 %2B q^2 -r^2 - s^2) \,$

which, regrouping, is of the form 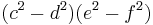$(c^2-d^2)(e^2-f^2)$

$= ( (r%2Bs)^2 - (p-q)^2 )( (p%2Bq)^2 - (r-s)^2 ) \,$

hence yielding four linear factors: 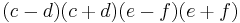$(c-d)(c%2Bd)(e-f)(e%2Bf)$

$= (q%2Br%2Bs-p)(p%2Br%2Bs-q)(p%2Bq%2Bs-r)(p%2Bq%2Br-s). \,$

Introducing 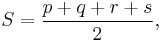$S = \frac{p%2Bq%2Br%2Bs}{2},$

$16(\mbox{Area})^2 = 16(S-p)(S-q)(S-r)(S-s). \,$

Taking the square root, we get

$\mbox{Area} = \sqrt{(S-p)(S-q)(S-r)(S-s)}.$

Extension to non-cyclic quadrilaterals

In the case of non-cyclic quadrilaterals, Brahmagupta's formula can be extended by considering the measures of two opposite angles of the quadrilateral:

$K=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\theta}$

where θ is half the sum of two opposite angles. (The pair is irrelevant: if the other two angles are taken, half their sum is the supplement of θ. Since cos(180° − θ) = −cosθ, we have cos²(180° − θ) = cos²θ.) It follows from this fact that the area of a cyclic quadrilateral is the maximum possible area for any quadrilateral with the given side lengths. This more general formula is sometimes known as Bretschneider's formula.

It is a property of cyclic quadrilaterals (and ultimately of inscribed angles) that opposite angles of a quadrilateral sum to 180°. Consequently, in the case of an inscribed quadrilateral, θ = 90°, whence the term

$abcd\cos^2\theta=abcd\cos^2 \left(90^\circ\right)=abcd\cdot0=0, \,$

giving the basic form of Brahmagupta's formula.

A related formula, which was proved by Coolidge, also gives the area of a general convex quadrilateral. It is^[1]

$K=\sqrt{(s-a)(s-b)(s-c)(s-d)-\textstyle{1\over4}(ac%2Bbd%2Bpq)(ac%2Bbd-pq)}\,$

where p and q are the lengths of the diagonals of the quadrilateral. In a cyclic quadrilateral, 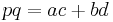$pq=ac%2Bbd$ according to Ptolemy's theorem, and the formula of Coolidge reduces to Brahmagupta's formula.

Related theorems

Heron's formula for the area of a triangle is the special case obtained by taking d = 0.
The relationship between the general and extended form of Brahmagupta's formula is similar to how the law of cosines extends the Pythagorean theorem.

External links

MathWorld: Brahmagupta's formula

References

^ J. L. Coolidge, "A Historically Interesting Formula for the Area of a Quadrilateral", American Mathematical Monthly, 46 (1939) pp. 345-347.

This article incorporates material from proof of Brahmagupta's formula on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.